LSM-tree 性能优化：Monkey, Dostoevsky

最近几天看了两篇 LSM-tree 优化的文章，简单总结一下。

本文涉及到的两篇文章分别是：

• Monkey: Optimal Navigable Key-Value Store
• Dostoevsky: Better Space-Time Trade-Offs for LSM-Tree Based Key-Value Stores via Adaptive Removal of Superfluous Merging

在介绍这两篇文章之前，我们先来看一下 LSM-tree 的时间和空间复杂度。

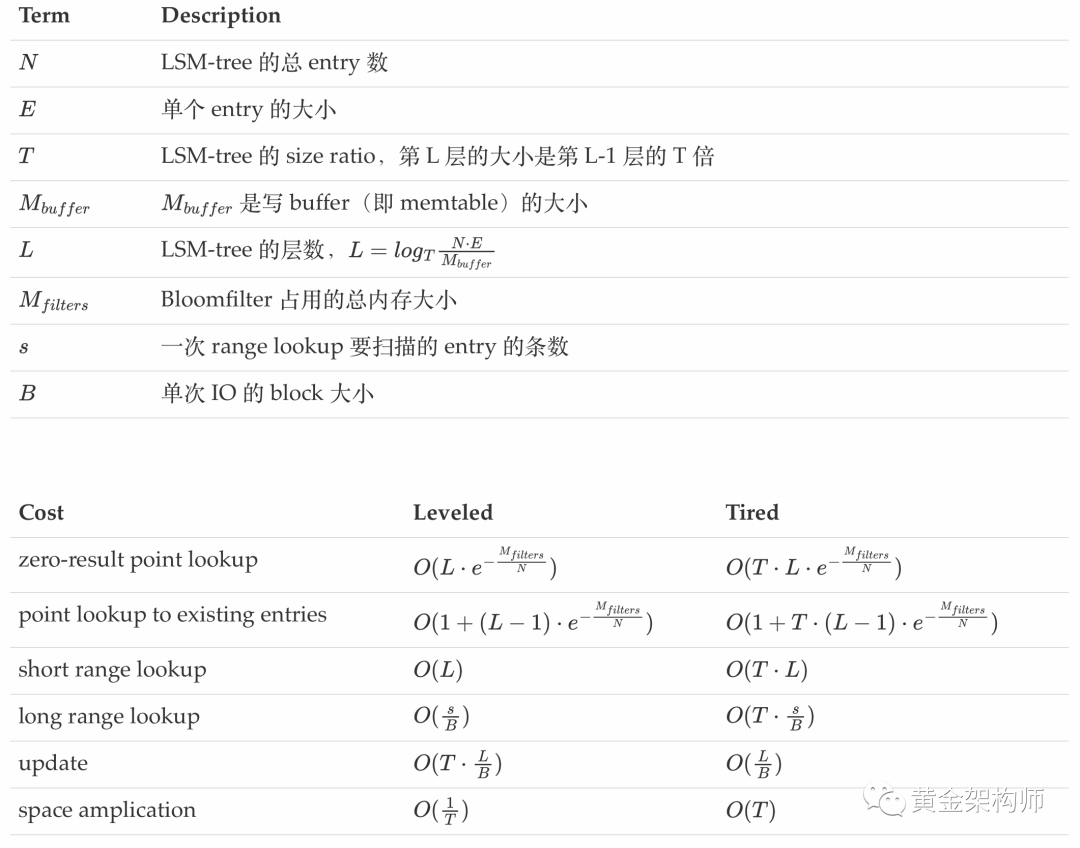
上图有几处需要解释一下：

• lookup 这里区分了 zero-result point lookup（没查到数据）和 point lookup to existing entries（确实查到一条数据）。这里把 zero-result point lookup 专门拎出来是考虑到这种情况也比较常见，考虑一下 insert if not exists 的场景。
• $O(e^{-\frac{M_{filters}}{N}})$ 是根据 Bloomfilter 的假阳性概率得来的，Bloomfilter 的假阳性概率： $FPR(false\ positive\ rate) = e^{-\frac{bits}{entries} \cdot (ln{2})^2}$，bits 为分配的内存 bit 数，entries 为 entry 条数。上图假定 LSM-tree 每一层的假阳性率都是一样的，业界的 LSM-tree 实现都是如此（e.g., RocksDB 的 Bloomfilter 每一层都是 10bits/entry）
• short range lookup 和 long range lookup 区分方式：如果满足 $\frac{s}{B} > 2 \cdot L$ 就是 long range lookup，否则就是 short range lookup。

接下来我们开始说 Monkey。

Monkey 主要优化的是 point lookup 的开销。Monkey 的主要思想：在 Bloomfilter 的总内存配额不变的情况下，通过调整 LSM-tree 不同层 Bloomfilter 的内存大小（假阳性率），降低 point lookup 的开销。

我们从直觉上想一下，业界的 LSM-tree 实现方案的每一层的假阳性率都是一样的。最大的层需要通过很大的内存实现 ${e^{-X}}$ 的假阳性率，最小的层通过很少的内存就能实现 ${e^{-X}}$ 。而每一层对总的 point lookup 的开销的贡献是一样大的（对于 Leveled Compaction，都是 $O(e^{-X})$，这里的 $X$ 简单代指上文图中的$\frac{M_{filters}}{N}$，下文同）。由此可见，越小的层的内存性价比越高，我们何不降低一下较大的层的内存，把它分配给较小的层，这样在我们内存成本（总量）不变的情况下，内存利用更高效，lookup 开销更小。

Monkey 通过一大堆数学论证，最终得出的结论是：我们只要让 LSM-tree 从小层到大层的 Bloomfilter 的假阳性率指数递增（几何级数），就能得到最优的开销。如上图，按照这个做法，最终 zero-point point lookup 的开销就是：$O(e^{-X}) = O(\frac{e^{-X}}{R^0}) + O(\frac{e^{-X}}{R^1}) + \cdot\cdot\cdot + O(\frac{e^{-X}}{R^{L - 1}})$

这个开销相比于优化前的开销$ O(L\cdot e^{-\frac{M_{filters}}{N}})$，优化掉了一个系数 $L$，效果非常显著。

我们现在更新一下上文的开销表格，在 Monkey 的帮助下，不管是 Leveled 还是 Tired，不管是 zeor-result point lookup 还是 point lookup to existing entry，都得到了优化。新的开销表格如下（优化的项已标红）：

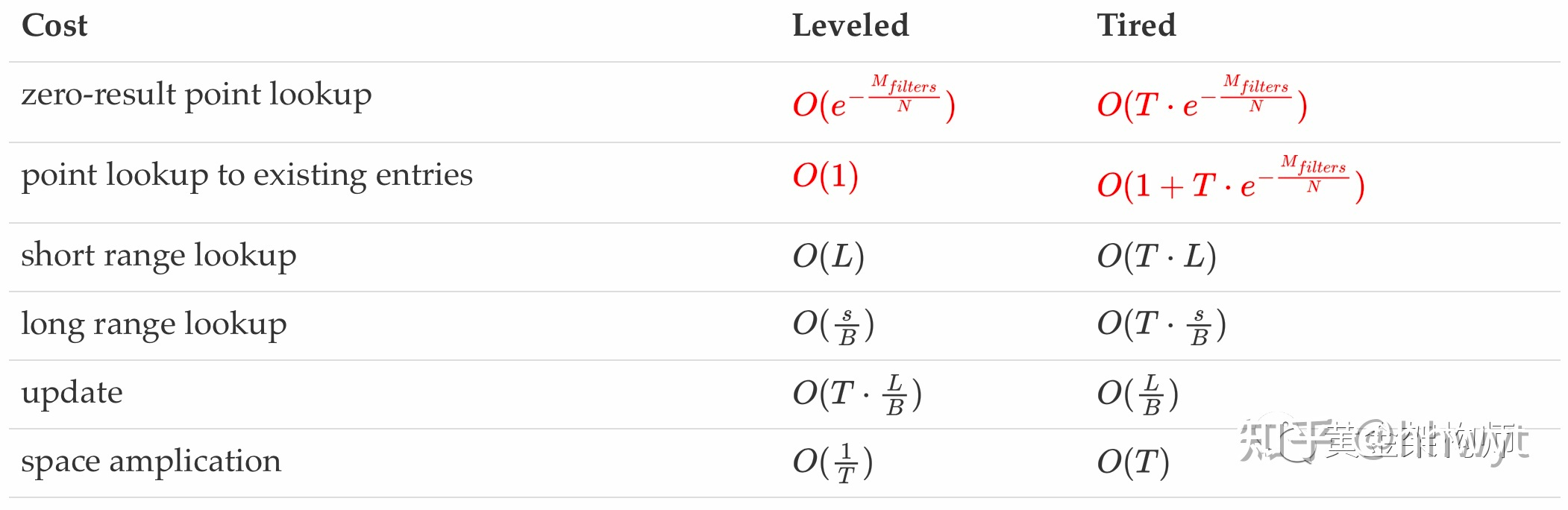
接下来我们再说说 Dostoevsky。 Dostoevsky 的主要思想是：通过折中 Tired 和 Leveled 两个方案（最大层用 Leveled，其余层用 Tired），牺牲少许 short range lookup 的性能，来换取更好的 update 性能。这个方案更适合写密集型场景。

在 Dostoevsky + Monkey 方案下（论文命名为 Lazy Leveled），LSM-tree 最终的时间空间复杂度如下图：

总结一下，Monkey 的效果：

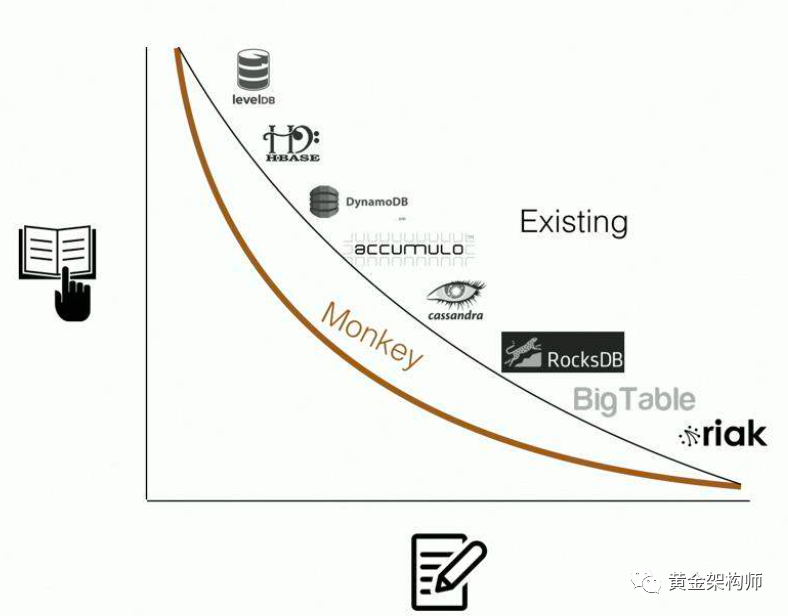
(横坐标为 update 开销，纵坐标为 lookup 开销)

相对于业界 LSM-tree 实现，Monkey 通过调整 LSM-tree 不同层 Bloomfilter 的假阳性率，在没有增加 update 开销的情况下，减小了 lookup 开销，换句话说，在没有内卷别人的情况下，做大了蛋糕，大家获得共赢。

Monkey + Dostoevsky 的效果：

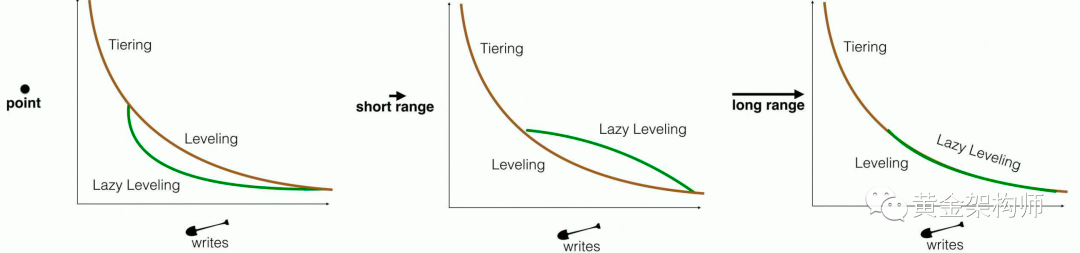相对于业界 LSM-tree 实现，Dostoevkey 通过让 LSM-tree 最后一层用 Leveled，其余层用 Tired 方案，获得了更好的 update 性能（虽然增加了一点 short range lookup 的开销），虽然没有像 Monkey 那样把蛋糕做大了，但分蛋糕的方式调整了一下，也能让有些吃蛋糕的人（写密集型场景）更爽一些，也是有它的应用场景的。

文末打个广告，欢迎大家也关注一下我的微信公众号，搜索「黄金架构师」，非常感谢！